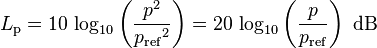Sound
Sound
Lately I have been wondering if there is a physical limit to how loud a sound can get. And to clarify, I am not referring to the audible range the human ear can receive, instead I am asking if there is a point at which sound cannot get any louder because it has reached its limit. Anything louder would be dubbed physically impossible.
- Chris Peterson
- Abominable Snowman
- Posts: 18594
- Joined: Wed Jan 31, 2007 11:13 pm
- Location: Guffey, Colorado, USA
- Contact:
Re: Sound
There is no intrinsic limit on the level of acoustic energy, although you might very reasonably say there are practical limits- for example, when the energy levels are high enough to dissociate molecules into atoms, or atoms into their constituent particles, or even to produce a fusing plasma. But these sort of state changes, while representing limits of acoustic energy in some sense of the concept, don't actually limit the total energy in the system.The Alien wrote:Lately I have been wondering if there is a physical limit to how loud a sound can get. And to clarify, I am not referring to the audible range the human ear can receive, instead I am asking if there is a point at which sound cannot get any louder because it has reached its limit. Anything louder would be dubbed physically impossible.
I suppose it is fair to say that the acoustic energy of a system can never exceed the mass-energy equivalence of that system. In other words, if every particle in the system is traveling at c, the system can't get any "louder". But I'm talking about a closed system here... add some more mass, and you can have more acoustic energy as well.
Chris
*****************************************
Chris L Peterson
Cloudbait Observatory
https://www.cloudbait.com
*****************************************
Chris L Peterson
Cloudbait Observatory
https://www.cloudbait.com
- neufer
- Vacationer at Tralfamadore
- Posts: 18805
- Joined: Mon Jan 21, 2008 1:57 pm
- Location: Alexandria, Virginia
Re: Sound
The Alien wrote:
Lately I have been wondering if there is a physical limit to how loud a sound can get. And to clarify, I am not referring to the audible range the human ear can receive, instead I am asking if there is a point at which sound cannot get any louder because it has reached its limit. Anything louder would be dubbed physically impossible.
In air at STP the root-mean-square sound pressure p cannot exceed {101325/sqrt(2)} Pahttp://en.wikipedia.org/wiki/Sound wrote:
<<Sound pressure is the difference, in a given medium, between average local pressure and the pressure in the sound wave. A square of this difference (i.e., a square of the deviation from the equilibrium pressure) is usually averaged over time and/or space, and a square root of this average provides a root mean square (RMS) value. For example, 1 Pa RMS sound pressure (94 dBSPL) in atmospheric air implies that the actual pressure in the sound wave oscillates between (1 atm - sqrt{2} Pa) and (1 atm + sqrt{2} Pa), that is between 101323.6 and 101326.4 Pa. Such a tiny (relative to atmospheric) variation in air pressure at an audio frequency is perceived as a deafening sound, and can cause hearing damage.
As the human ear can detect sounds with a wide range of amplitudes, sound pressure is often measured as a level on a logarithmic decibel scale. The sound pressure level (SPL) or Lp is defined as
where p is the root-mean-square sound pressure and pref is a reference sound pressure. Commonly used reference sound pressures, defined in the standard ANSI S1.1-1994, are 20 µPa in air and 1 µPa in water. Without a specified reference sound pressure, a value expressed in decibels cannot represent a sound pressure level.>>
such that the actual pressure in the sound wave oscillates between 2 atm and 0 atm.
Ergo: Maximum Lp = 20 log({101325/sqrt(2)}x 10 6/{20}) = 191 dB
Art Neuendorffer