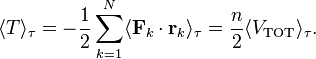http://en.wikipedia.org/wiki/Virial_theorem wrote:
<<
The word "virial" derives from vis, the Latin word for "force" or "energy", and was given its technical definition by Clausius in 1870. In mechanics, the virial theorem provides a general equation relating the average over time of the total kinetic energy,

, of a stable system consisting of N particles, bound by potential forces, with that of the total potential energy,
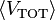
, where angle brackets represent the average over time of the enclosed quantity.
Mathematically, the theorem states:

where F
k represents the force on the kth particle, which is located at position r
k.
If the force between any two particles of the system results from a potential energy V(r) = αr
n that is proportional to some power n of the inter-particle distance r, the virial theorem adopts a simple form:

. Thus, twice the average total kinetic energy

equals n times the average total potential energy
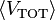
. Whereas V(r) represents the potential energy between two particles, V
TOT represents the total potential energy of the system, i.e., the sum of the potential energy V(r) over all pairs of particles in the system. A common example of such a system is a star held together by its own gravity, where n equals −1.
Although the virial theorem depends on averaging the total kinetic and potential energies, the presentation here postpones the averaging to the last step. The significance of the virial theorem is that it allows the average total kinetic energy to be calculated even for very complicated systems that defy an exact solution, such as those considered in statistical mechanics; this average total kinetic energy is related to the temperature of the system by the equipartition theorem. However, the virial theorem does not depend on the notion of temperature and holds even for systems that are not in thermal equilibrium. The virial theorem has been generalized in various ways, most notably to a tensor form.
History of the virial theorem
In 1870, Rudolf Clausius delivered the lecture "On a Mechanical Theorem Applicable to Heat" to the Association for Natural and Medical Sciences of the Lower Rhine, following a 20 year study of thermodynamics. The lecture stated that the mean vis viva of the system is equal to its virial, or that the average kinetic energy is equal to 1/2 the average potential energy. The virial theorem can be obtained directly from Lagrange's Identity as applied in classical gravitational dynamics, the original form of which was included in his "Essay on the Problem of Three Bodies" published in 1772. Karl Jacobi's generalization of the identity to n bodies and to the present form of Laplace's identity closely resembles the classical virial theorem. However, the interpretations leading to the development of the equations were very different, since at the time of development, statistical dynamics had not yet unified the separate studies of thermodynamics and classical dynamics. The theorem was later utilized, popularized, generalized and further developed by persons such as James Clerk Maxwell, Lord Rayleigh, Henri Poincaré, Subrahmanyan Chandrasekhar, Enrico Fermi, Paul Ledoux and Eugene Parker. Fritz Zwicky was the first to use the virial theorem to deduce the existence of unseen matter, which is now called dark matter. As another example of its many applications, the virial theorem has been used to derive the Chandrasekhar limit for the stability of white dwarf stars. Lord Rayleigh published a generalization of the virial theorem in 1903. Although derived for classical mechanics, the virial theorem also holds for quantum mechanics.
...........................................................................
For power-law forces with an exponent n, the general equation holds
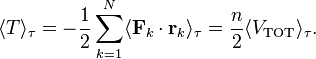
For gravitational attraction, n equals −1 and the average kinetic energy equals half of the average negative potential energy

This general result is useful for complex gravitating systems such as solar systems or galaxies.
A simple application of the virial theorem concerns galaxy clusters. If a region of space is unusually full of galaxies, it is safe to assume that they have been together for a long time, and the virial theorem can be applied. Doppler measurements give lower bounds for their relative velocities, and the virial theorem gives a lower bound for the total mass of the cluster, including any dark matter.
The averaging need not be taken over time; an ensemble average can also be taken, with equivalent results.>>



 , of a stable system consisting of N particles, bound by potential forces, with that of the total potential energy,
, of a stable system consisting of N particles, bound by potential forces, with that of the total potential energy, 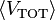 , where angle brackets represent the average over time of the enclosed quantity.
, where angle brackets represent the average over time of the enclosed quantity. 
 . Thus, twice the average total kinetic energy
. Thus, twice the average total kinetic energy