Starship Asterisk*

http://apod.nasa.gov/apod/ap090730.html wrote:
Explanation: The July 22nd total solar eclipse was the longest of the 21st century. From the point of maximum eclipse along the Moon's shadow track across the Pacific Ocean, the Moon completely blocked the Sun for a total of 6 minutes and 39 seconds. But from the deck of this cruise ship the duration of the total eclipse phase was extended to a whopping 6 minutes and 42 seconds by the ship's motion along the shadow track.

1) Estimate the approximate speed of the cruise ship in knots.

• (Try to do it in your head if you can).

2) How fast would you have to travel to make the eclipse motion stop totally?

-------------------------------------------------------------------

• _The Pied Piper Of Hamelin_ Epilogue by Robert Browning
  
  Alas, alas for Hamelin!
  There came into many a burgher's pate
  A text which says, that Heaven's Gate
  Opes to the Rich at as easy rate
  As the needle's eye takes a camel in!
  The Mayor sent East, West, North, and South,
  To offer the Piper, by word of mouth,
  Wherever it was men's lot to find him,
  Silver and gold to his heart's content,
  If he'd only return the way he went,
  And bring the children behind him.
  But when they saw 'twas a lost ENDEAVOUR,
  And Piper and dancers were gone for ever,
  They made a decree that lawyers never
  Should think their records dated duly
  If, after the day of the month and year,
  These words did not as well appear,
  "And so long after what happened here
  On the Twenty-second of July,
  Thirteen hundred and seventy-six":
  And the better in memory to fix
  The place of the children's last retreat,
  They called it, the Pied Piper's Street—
  Where any one playing on pipe or tabor
  Was sure for the future to lose his labour.
  Nor suffered they hostelry or tavern
  To shock with mirth a street so solemn;
  But opposite the place of the cavern
  They wrote the story on a column,
  And on the great Church-Window painted
  The same, to make the world acquainted
  How their children were stolen away;
  And there it stands to this very day.
  And I must not omit to say
  That in Transylvania there's a tribe
  Of alien people that ascribe
  The outlandish ways and dress
  On which their neighbours lay such stress,
  To their fathers and mothers having risen
  Out of some subterraneous prison
  Into which they were trepanned
  Long time ago in a mighty band
  Out of Hamelin town in Brunswick land,
  But how or why, they don't understand.

-------------------------------------------------------------------

neufer wrote:

http://apod.nasa.gov/apod/ap090730.html wrote:
Explanation: The July 22nd total solar eclipse was the longest of the 21st century. From the point of maximum eclipse along the Moon's shadow track across the Pacific Ocean, the Moon completely blocked the Sun for a total of 6 minutes and 39 seconds. But from the deck of this cruise ship the duration of the total eclipse phase was extended to a whopping 6 minutes and 42 seconds by the ship's motion along the shadow track.

1) Estimate the approximate speed of the cruise ship in knots.

• (Try to do it in your head if you can).

2) How fast would you have to travel to make the eclipse motion stop totally?

If the ship was travelling at K knots when this photo was taken, and it only managed to extend totality by 3 seconds, it would have to travel at a speed of about 133 x K knots (6 min. 39 sec. divided by 3 sec. = 133) to stop it in its tracks. What a rush!

Rob

rstevenson wrote:

neufer wrote:2) How fast would you have to travel to make the eclipse motion stop totally?

If the ship was travelling at K knots when this photo was taken, and it only managed to extend totality by 3 seconds, it would have to travel at a speed of about 133 x K knots (6 min. 39 sec. divided by 3 sec. = 133) to stop it in its tracks. What a rush!

• Out on the briny with a moon big and shiny
  creating a large umbra cone.
  I'd love to get on a fast boat from China,
  all by myself, alone.

Since I am not shy about exposing my ignorance, and too proud of my ability for mental arithmetic I'll bite. After all, here is a chance to learn something!

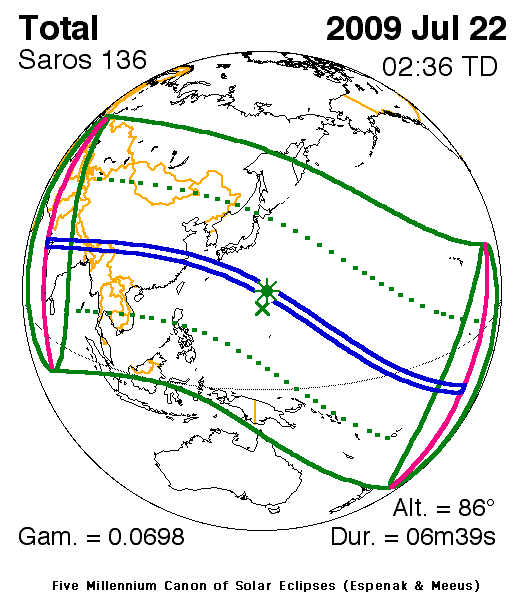
After wiggling the picture in my mind for a while I have "almost" convinced myself that the ship is mostly fighting the speed of Earth's rotation. The speed of rotation at the equator is 360 degrees/24 hours, or 15 degrees/hr. 15 degrees = 900 minutes, so the rotational speed of any point on the equator is 900 knots. According to the map that Art showed, the ship was at latitude theta somewhere between 20 to 30 degrees North. This figure could be off - would have helped to show the tropics on that map . Let's go with cos(theta)=0.9 fully knowing that this is not accurate. So the speed of the shadow on the surface of the Earth would be something like 800 knots (could be 830, could be 760??). As was pointed out be rstevenson 3 seconds outf 399 is a fraction of 1/133, and 800/133=6, so at this point I would go with a cruising speed of 6 knots. The ship could probably go faster than that, but may be 6 knots was the limit for keeping it steady for photography or whatever.

But I'm not entirely happy with this figure. It is based on something like the shadow being a tube (more accurately a section of a sharp cone, but forget that) pointing at the Earth, when in fact the axis of the cone of the shadow itself is turning relative to Earth as well. I would like to say that the shadow is turning at an angular speed that equals the difference between the angular speeds of the Moon and the Sun (given that an eclipse occured!). So here we go again. Start the arithmetic with a figure of 30 days from full moon to full moon, so 12 degrees per day,... Wait a second - this should give one thirtieth of the angular speed we just computed. I can live with an error of 3 per cent here, so ignore this.

Hmm. The motion of the shadow is not only East-West, but I' suffering from a mild hangover, so I'll stop here and gamble on 6 knots.

Cheers,

Jyrki

When first I came to Asterisk
An answer there to find
The postings I discovered there
Overwhelmed my mind
The learned and quotidian quotes
Like arrows pierced my breast
I beat a hasty exit
But could not let it rest...
(apologies to Joan Baez)

As I'm more engineer than scientist, that's my approach here. There's an advantage to that; engineers deal a lot in approximations, and sometimes that's all you need. For instance, common electronics components have a tolerance of +/- 10%, thus a '1000 ohm' resistor may have an actual value between 900 and 1100 ohms - so what's the point of a more precise calculation? Carefully chosen approximations can make calculations significantly easier to do (and thus less prone to error) and the inaccuracies can offset one another, giving a more accurate result than you might think. Here we go:

Assumptions:
1) The moon's orbital distance from the earth is about 235,000 miles.
2) The shadow of the moon moves across the face of the Earth at approximately the same speed as the moon moves in its orbit, since the Earth-Moon distance is swamped in the Earth-Sun distance.

Duration of the eclispe for a stationary observer: 6 min 39 sec.
Duration of the eclispe on the ship: 6 min 42 sec.

First, convert the times to seconds:
6 min 39 sec ==> 399 seconds
6 min 42 sec ==> 402 seconds

Next, calculate the moon's orbital velocity:
Length of orbit is 235,000 x 2 x pi (3.14) ==> 1,475,800 miles
Miles per day is 1,475,800 / 28 ==> 52,707
Miles per hour is 52,707 / 24 ==> 2,196
Miles per second is 2,196 / 3,600 ==> 0.61 miles per second

Next, how far did the moon (and its shadow) move in those extra 3 seconds?
0.61 miles/second x 3 seconds ==> 1.83 miles

So the ship moved 1.83 miles in 402 seconds.
1.83 / 402 ==> .00455 miles per second
.00455 x 3600 seconds per hour ==> 16.4 miles per hour

A completely reasonable answer for a modern cruise ship.

Also consider that, lacking an external reference such as a GPS, currents and winds would likely introduce some uncertainty in the actual speed of the ship. So if my answer is at all correct, the error introduced by my approximations might well be within the range of uncertainty of the ship's measured velocity.

I'd enjoy seeing the number a more precise - and learned - calculation would produce. And as an exercise, try rounding things significantly, like 3 for pi, 30 for the number of days in a lunar month, 25 hours in a day, try to do it in your head, see how close your result is.

Michael

Hi Michael,

Good figurin'.

Up above I said the ship would have to travel about 133 times faster to stop totality in its tracks. Comparing your 0.61 mps x 60 x 60 = roughly 2200 mph to your 16.4 mph x my factor of 133 = roughly 2200, I can see I was in the ballpark. I'm not sure how stable a camera platform a ship would be travelling at that rate though.

Rob

Forgot Art wanted the answer in knots (geez, I'm already in knots):

16.4 miles per hour / 1.15 knots/mph ==> 14.3 knots.

Michael

I did not even try to figure it out. I've already got way tooooooo many knots in my head