Page 5 of 6
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 4:27 am
by Nitpicker
owlice wrote:What are the chances that two of the three main statistics on the Asterisk home page (Total posts, total topics, total members) are prime numbers at any given time? As has happened in the past, tonight I noticed that two of them were prime (Total posts 132721 • Total topics 12577); it's inevitable that this circumstance should occur, but how often?
The rate will vary.

It has been quite some time since I messed around with primes. I want to say that the rate will decrease over time, but I'm not even sure about that any more.
Not much of an answer. Hmmm. If it helps to keep the numbers nice and prime, you may delete this post.

Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 4:29 am
by geckzilla
(total number of primes / total number of non-primes) * average posts per day * average topics per day

Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 4:39 am
by owlice
The Register wrote:Okay maths wonks: PRIME TIME has arrived
Cosmic prime number alignment due just after lunchtime today
By Simon Sharwood, 7th November 2013
Every Reg reader knows that a prime number is divisible only by one and itself.
But did you also know that today is a big day for prime numbers?
When the clock ticks over to 2:03:05 on November the 7th, 2013, the universe will experience an unusual alignment of prime numbers as the time becomes 02:03:05:07:11:13.
More here:
http://www.theregister.co.uk/2013/11/07 ... s_arrived/
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 11:37 am
by Nitpicker
Now that I think about it some more, the largest integer this forum software could count up to is likely to be:
2,147,483,647 ... the largest 4 byte signed integer: (2^31)-1 [which I recall vaguely, is prime]
or at a long shot:
4,294,967,295 ... the largest 4 byte unsigned integer: (2^32)-1
or at a really long shot, maybe a 64 bit variant.
...
Whichever the number, the total number of integers and total number of primes are both finite here on the Starship ... and geckzilla's faux-formula, above, is not quite as silly as it looks (although it is still quite wrong). It also provides another example of how computers make life easier -- none of this icky infinite business making itself unpleasant (don't mention divide by zero, please).
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 12:10 pm
by geckzilla
phpBB uses mysql's unsigned mediumint for most large numbers, making 16777215 the largest ID value. However, I would definitely change the database schema if it ever came to that.
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 12:14 pm
by Nitpicker
Tsk, tsk, tsk. It just gets easier and easier.

Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 12:22 pm
by geckzilla
But a lot less satisfying. Three bytes is hardly enough to fill one's stomach.
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 12:36 pm
by Nitpicker
It is owlice I feel bad for. Imagine her fondness for 2,147,483,647. The mind reels.
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 1:43 pm
by rstevenson
owlice wrote:The Register wrote:Okay maths wonks: PRIME TIME has arrived
Cosmic prime number alignment due just after lunchtime today
By Simon Sharwood, 7th November 2013
Every Reg reader knows that a prime number is divisible only by one and itself.
But did you also know that today is a big day for prime numbers?
When the clock ticks over to 2:03:05 on November the 7th, 2013, the universe will experience an unusual alignment of prime numbers as the time becomes 02:03:05:07:11:13.
I find it hard to express how silly I find that last statement. That string of digits (in what is only our most commonly used counting system) is not even universal here on Earth, since it is a numerical expression of just one of our date systems, and it even leaves out two digits in the year part of the expression. Talk about cherry picking your numbers to make a point, and a dubius point at that: "the
universe will experience"?
Universe??? 
Rob
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 2:11 pm
by Chris Peterson
rstevenson wrote:owlice wrote:The Register wrote:Okay maths wonks: PRIME TIME has arrived
Cosmic prime number alignment due just after lunchtime today
By Simon Sharwood, 7th November 2013
Every Reg reader knows that a prime number is divisible only by one and itself.
But did you also know that today is a big day for prime numbers?
When the clock ticks over to 2:03:05 on November the 7th, 2013, the universe will experience an unusual alignment of prime numbers as the time becomes 02:03:05:07:11:13.
I find it hard to express how silly I find that last statement. That string of digits (in what is only our most commonly used counting system) is not even universal here on Earth, since it is a numerical expression of just one of our date systems, and it even leaves out two digits in the year part of the expression. Talk about cherry picking your numbers to make a point, and a dubius point at that: "the
universe will experience"?
Universe??? :roll:
Rob
Yes, that's silly. How could they have overlooked the fact that at nearly the same time the age of the Universe will be a prime number of Planck units. I'd write the number out here for you to check yourself, but it has nearly 10
61 digits, and even assuming sufficient memory on the Asterisk computer, it would require a minimum time of the age of the Universe to type, and that long again for you to read. And I hope you have fast Internet! So you'll just have to take my word for the primeness of the time.
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 3:00 pm
by Nitpicker
Chris Peterson wrote:Yes, that's silly. How could they have overlooked the fact that at nearly the same time the age of the Universe will be a prime number of Planck units. I'd write the number out here for you to check yourself, but it has nearly 1061 digits, and even assuming sufficient memory on the Asterisk computer, it would require a minimum time of the age of the Universe to type, and that long again for you to read. And I hope you have fast Internet! So you'll just have to take my word for the primeness of the time.
And ... pip ... there it was. Woof! That sure was one memorable unit of Planck time. Makes me feel like a
Planck normalised universal constant ... at 1 with the universe.
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 3:18 pm
by Beyond
haha, I'm just glad that I'm
Beyond all this


Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 3:22 pm
by geckzilla
A weary catchphrase.
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 3:32 pm
by Beyond
Sorry, it's all i got. I gotta be me... i gotta be me, no matter how b-o-r-i-n-g, if that's all you c.

Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 4:22 pm
by neufer
Chris Peterson wrote:
Yes, that's silly. How could they have overlooked the fact that at nearly the same time the age of the Universe will be a prime number of Planck units. I'd write the number out here for you to check yourself, but it has nearly 1061 digits,
How could Chris have overlooked the fact that:
- 1) The Big Bang occurred approximately 13.798 ± 0.037 billion years ago,
- which is thus considered the age of the universe.
2) The age of the Universe (~ 8.077 x 1060 tP) in Planck units has exactly 61 digits.
3) The probability that this is a prime number (at any given instant) ~ 1 / ln(8.077 x 1060) is ~ 1 in 140.
http://en.wikipedia.org/wiki/Planck_time wrote:
<<In physics, the Planck time (t
P) is the unit of time in the system of natural units known as Planck units.
It is the time required for light to travel, in a vacuum, a distance of 1 Planck length.
The Planck time is defined as:
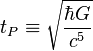 ≈ 5.39106(32) × 10−44 s
≈ 5.39106(32) × 10−44 s >>
Re: Forum Statistic - What's the odds?
Posted: Thu Nov 07, 2013 11:12 pm
by Nitpicker
neufer wrote:The age of the Universe in Planck units has exactly 61 digits
You're right. Only 61 digits. A mere trifle for a good arbitrary precision library. There are probably lawyers willing to sue over illegal prime numbers bigger than that.
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 5:34 am
by neufer
Nitpicker wrote:neufer wrote:
The age of the Universe in Planck units has exactly 61 digits
You're right. Only 61 digits. A mere trifle for a good arbitrary precision library.
There are probably lawyers willing to sue over illegal prime numbers bigger than that.
http://en.wikipedia.org/wiki/Largest_known_prime_number wrote:
As of October 2013, the largest known prime number is 2
57,885,161 − 1, a number with 17,425,170 digits.
It would require 4,647 pages to display this number in base 10 with 75 digits per line and 50 lines per page.
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 6:12 am
by Nitpicker
neufer wrote: http://en.wikipedia.org/wiki/Largest_known_prime_number wrote:
As of October 2013, the largest known prime number is 2
57,885,161 − 1, a number with 17,425,170 digits.
It would require 4,647 pages to display this number in base 10 with 75 digits per line and 50 lines per page.
It is Friday afternoon here and I'm beginning to loosen up. If I were to similarly loosen my semantics a fraction, I could say that Wikipedia claims the largest known prime number is divisible by 4647, 75 and 50, and also by pages, digits and lines.
Have a good weekend.
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 8:48 am
by owlice
Nitpicker wrote:It is owlice I feel bad for. Imagine her fondness for 2,147,483,647. The mind reels.
That number doesn't call out to me. There are some primes I really like (10501, for example, and 50101), and winged primes are fun (such as 78487, and yes, I also like palindomes), but 2147483647? A fine prime, but not a pretty one.
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 8:51 am
by owlice
And BTW: Total topics 12589.

Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 10:08 am
by Nitpicker
owlice wrote:That number doesn't call out to me. There are some primes I really like (10501, for example, and 50101), and winged primes are fun (such as 78487, and yes, I also like palindomes), but 2147483647? A fine prime, but not a pretty one.
Owlice, the only big prime I know well, 2147483647, just called me. It sounded pretty upset -- close to overflowing with negativity.
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 3:06 pm
by neufer
owlice wrote:
That number doesn't call out to me. There are some primes I really like (10501, for example, and 50101), and winged primes are fun (such as 78487, and yes, I also like palindomes), but 2147483647? A fine prime, but not a pretty one.
- Au contrair, mon ami

http://en.wikipedia.org/wiki/2147483647 wrote:
The number 2,147,483,647 is the eighth Mersenne prime, equal to 2
31 − 1.
It is one of only four known double Mersenne primes.
There are probably no other double Mersenne primes than the four known.
The primality of this number was proven by Leonhard Euler, who reported the proof in a letter to Daniel Bernoulli written in 1772. Euler used trial division, improving on Cataldi's method, so that at most 372 divisions were needed.
In 1811, Peter Barlow, not anticipating future interest in prime numbers, wrote (in An Elementary Investigation of the Theory of Numbers): "
Euler ascertained that 231 − 1 = 2147483647 is a prime number; and this is the greatest at present known to be such, and, consequently, the last of the above perfect numbers [i.e., 230(231 − 1)], which depends upon this, is the greatest perfect number known at present, and probably the greatest that ever will be discovered; for as they are merely curious, without being useful, it is not likely that any person will attempt to find one beyond it."
In fact a larger prime, 2
127 − 1, was not found in 1876 (by Lucas)
(In 1883 Pervushin found the prime 2
61 − 1.)
The number 2,147,483,647 is also the maximum value for a 32-bit signed integer in computing. It is therefore the maximum value for variables declared as int in many programming languages running on popular computers, and the maximum possible score, money etc. for many video games. The appearance of the number often reflects an error, overflow condition, or missing value. The data type
time_t, used on operating systems such as Unix, is a 32-bit signed integer counting the number of seconds since the start of the Unix epoch (midnight UTC of 1 January 1970). The latest time that can be represented this way is 03:14:07 UTC on Tuesday, 19 January 2038 (corresponding to 2,147,483,647 seconds since the start of the epoch),
so that systems using a 32-bit time_t type are susceptible to the Year 2038 problem.>>
http://en.wikipedia.org/wiki/Double_Mersenne_number wrote:
In mathematics, a double Mersenne number is a Mersenne number of the form:
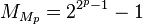
where p is a Mersenne prime exponent.
The sequence of double Mersenne numbers (
A077586 in OEIS) begins:
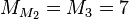

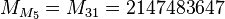

In the Futurama movie
The Beast with a Billion Backs, the double Mersenne number:

is briefly seen in "
an elementary proof of the Goldbach conjecture".
In the movie, this number is known as a "
martian prime".
-------------------------------------------------------------------------
A double Mersenne number that is prime is called a double Mersenne prime. Since a Mersenne number M
p can be prime only if p is prime, a double Mersenne number

can be prime only if M
p is itself a Mersenne prime. The first values of p for which M
p is prime are p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127. Of these,

is known to be prime for p = 2, 3, 5, 7. For p = 13, 17, 19, and 31, explicit factors have been found showing that the corresponding double Mersenne numbers are not prime. Thus, the smallest candidate for the next double Mersenne prime is
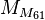
, or 2
2305843009213693951 − 1. Being approximately 1.695×10
694127911065419641, this number is far too large for any currently known primality test. It has no prime factor below 4×10
33.
-------------------------------------------------------------------------
The Catalan–Mersenne number conjecture
Write M(p) instead of

. A special case of the double Mersenne numbers, namely the recursively defined sequence
2, M(2), M(M(2)), M(M(M(2))), M(M(M(M(2)))), ... (sequence
A007013 in OEIS)
is called the Catalan–Mersenne numbers. It is said that Catalan came up with this sequence after the discovery of the primality of M(127)=M(M(M(M(2)))) by Lucas in 1876. Catalan conjectured that they, up to a certain limit, are all prime.
Although the first five terms (up to M(127)) are prime, no known methods can decide if any more of these numbers are prime (in any reasonable time) simply because the numbers in question are too huge, unless the primality of M(M(127)) is disproved.>>
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 3:09 pm
by Chris Peterson
I'm pretty sure this is how anybody would look after engaging in such a mathematical exercise.
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 3:34 pm
by geckzilla
He looks bald! Maybe he didn't like his head getting cold.
Re: Forum Statistic - What's the odds?
Posted: Fri Nov 08, 2013 3:40 pm
by Chris Peterson
geckzilla wrote:He looks bald! Maybe he didn't like his head getting cold.
"Mad" is the word I'd use. And I don't mean angry.
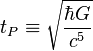


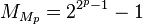
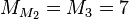

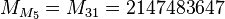

 can be prime only if Mp is itself a Mersenne prime. The first values of p for which Mp is prime are p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127. Of these,
can be prime only if Mp is itself a Mersenne prime. The first values of p for which Mp is prime are p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127. Of these, 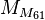 , or 22305843009213693951 − 1. Being approximately 1.695×10694127911065419641, this number is far too large for any currently known primality test. It has no prime factor below 4×1033.
, or 22305843009213693951 − 1. Being approximately 1.695×10694127911065419641, this number is far too large for any currently known primality test. It has no prime factor below 4×1033.  . A special case of the double Mersenne numbers, namely the recursively defined sequence
. A special case of the double Mersenne numbers, namely the recursively defined sequence