http://en.wikipedia.org/wiki/Double_Mersenne_number wrote:
In mathematics, a double Mersenne number is a Mersenne number of the form:
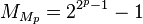
where p is a Mersenne prime exponent.
The sequence of double Mersenne numbers (
A077586 in OEIS) begins:
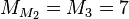

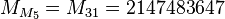

In the Futurama movie
The Beast with a Billion Backs, the double Mersenne number:

is briefly seen in "
an elementary proof of the Goldbach conjecture".
In the movie, this number is known as a "
martian prime".
-------------------------------------------------------------------------
A double Mersenne number that is prime is called a double Mersenne prime. Since a Mersenne number M
p can be prime only if p is prime, a double Mersenne number

can be prime only if M
p is itself a Mersenne prime. The first values of p for which M
p is prime are p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127. Of these,

is known to be prime for p = 2, 3, 5, 7. For p = 13, 17, 19, and 31, explicit factors have been found showing that the corresponding double Mersenne numbers are not prime. Thus, the smallest candidate for the next double Mersenne prime is
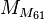
, or 2
2305843009213693951 − 1. Being approximately 1.695×10
694127911065419641, this number is far too large for any currently known primality test. It has no prime factor below 4×10
33.
-------------------------------------------------------------------------
The Catalan–Mersenne number conjecture
Write M(p) instead of

. A special case of the double Mersenne numbers, namely the recursively defined sequence
2, M(2), M(M(2)), M(M(M(2))), M(M(M(M(2)))), ... (sequence
A007013 in OEIS)
is called the Catalan–Mersenne numbers. It is said that Catalan came up with this sequence after the discovery of the primality of M(127)=M(M(M(M(2)))) by Lucas in 1876. Catalan conjectured that they, up to a certain limit, are all prime.
Although the first five terms (up to M(127)) are prime, no known methods can decide if any more of these numbers are prime (in any reasonable time) simply because the numbers in question are too huge, unless the primality of M(M(127)) is disproved.>>
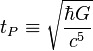


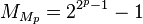
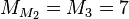

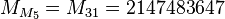

 can be prime only if Mp is itself a Mersenne prime. The first values of p for which Mp is prime are p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127. Of these,
can be prime only if Mp is itself a Mersenne prime. The first values of p for which Mp is prime are p = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127. Of these, 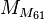 , or 22305843009213693951 − 1. Being approximately 1.695×10694127911065419641, this number is far too large for any currently known primality test. It has no prime factor below 4×1033.
, or 22305843009213693951 − 1. Being approximately 1.695×10694127911065419641, this number is far too large for any currently known primality test. It has no prime factor below 4×1033.  . A special case of the double Mersenne numbers, namely the recursively defined sequence
. A special case of the double Mersenne numbers, namely the recursively defined sequence